מחשוב בסיסי – חלק א'

מתמטיקה בינארית, לוגיקה בוליאנית ושערים לוגיים

מתמטיקה בינארית, לוגיקה בוליאנית ושערים לוגיים:

מתמטיקה של מספרים בינאריים היא פשוטה, כמעט באופן מזעזע, נשוב נוסטלגית לכיתה ג\':

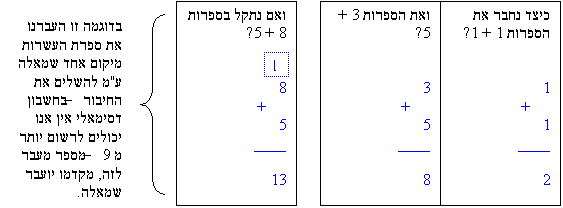
בדוגמה לעיל ניתן לראות כיצד אנו מחברים מספרים דסימאליים (על בסיס 10, "רגילים")

החוקים זהים בחיבור בינארי, יש לזכור כמובן כי לא נרשום מספר מעבר לאחד בחיבור בינארי:

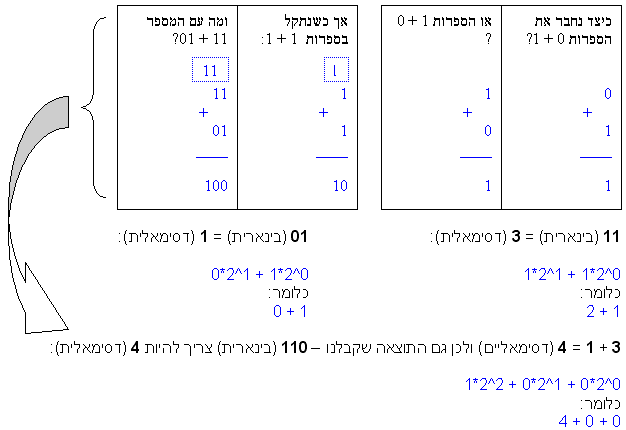
למרבה הפלא זה פועל… :-), הכלל: בחיבור בינארי אנו מעבירים שמאלה כל תוצאה הגדולה מ-1.

לוגיקה בוליאנית פשוטה אף יותר! מרגע שהפרינציפ מובן…, נראה כיצד היא פועלת:

ישנם 3 שערים בסיסים, השער הפשוט ביותר הינו שער "היפוך" (Inverter), שער NOT:

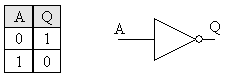
A מסמן את הכניסה, במקרה זה כניסה אחת בלבד (A).
Q מסמל את היציאה, זה נרשם "Q" במקום (O" Output") משום הצורך להבדילו מ "0" (אפס).
אי-כניסה של זרם (\'0\') תגרום להוצאת זרם (\'1\') וההפך – כניסה של זרם (\'1\') תגרום לאי-הוצאת זרם (\'0\').

שני השערים הבאים מורכבים טיפה יותר, שער AND:

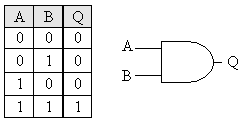
בשער זה רק עם גם A וגם B הינם \'1\' אז Q יהיה \'1\'.
בכל מצב אחר (אם רק A או רק B יהיה 1) Q יהיה \'0\'.

שער OR:

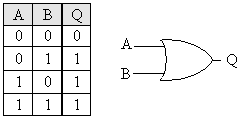
בשער זה דיי רק ש A או B יהיו 1, התוצאה תהיה 1.

אלו הם שלושת השערים הבסיסים, מהם ניתן לבנות את כל שאר השערים אולם מקובל להחשיב (תלוי מי מחשיב) בספירת השערים הבסיסית עוד 4 שערים נוספים (שכאמור ניתן לייצג ע"י שלושת השערים האלה..), ואלו הם ארבעת השערים הנוספים: